整体壁板因其轻质、高强、结构效率等优异的性能,被广泛应用于飞机机身、机翼部位等关键部件。目前,整体壁板常用的成形方法主要有喷丸、滚弯、压弯、蠕变时效成形等[1-3]。在同等强度设计要求下,高温钛合金网格筋壁板相较于传统的铝合金筋壁板壁厚更小、筋的高宽比更大,并通常具有单/双曲率的复杂曲面结构,属于薄壁整体复杂结构[4]。但由于高温钛合金多属非时效强化型合金、加工温度较高、加工窗口较窄、变形后回弹量大,采用常规冷变形或温热变形方法成形其网格筋整体壁板件对设备吨位要求较高、成形过程中易出现筋根部开裂和筋条上端失稳变形等成形缺陷,因此需探索新的成形方法。电脉冲辅助成形利用电致塑性效应显著降低成形载荷、提高材料的弯曲成形极限[5],有效避免成形过程中筋根部开裂问题;另一方面,可利用材料自阻产生的焦耳热温升快速提供热变形条件,弥补变形过程中的热损失,相较于电阻炉加热有望显著提高加热速度、降低能源消耗与工装成本[6]。然而,在电脉冲辅助成形过程中,由于电-热-力场不均匀分布特征和网格筋整体壁板压弯成形局部加载的特征,如电参数、变形参数、模具几何参数和加载路径设置不合理,可能导致壁板局部化变形严重、失稳起皱、开裂等缺陷。因此需要深入研究整体壁板电辅助成形变形行为,预测缺陷发生的时刻和位置,为整体壁板电辅助成形工艺设计提供依据。
关于整体壁板筋条失稳预测,国内外众多学者开展了深入研究。Yan[7,8]等提出了一种基于能量法、弹塑性力学和数值分析的压弯成形过程中加劲肋临界屈曲载荷的求解方法,并对铝合金高加劲肋整体板压弯成形断裂进行预测。Mallela等[9]利用神经网络准确预测了复合材料整体壁板的剪切失稳载荷。Li[10]等提出了一种新的分析方法来预测加筋板在循环平面载荷作用下的非线性应力应变曲线,对船舶等大型箱梁结构的渐进倒塌分析提供基础。Su[11]等研究了Ti6Al4V钛合金加筋板在平面剪切载荷作用下的结构行为。通过剪切试验,得到了试件的屈曲失稳、后屈曲过程和破坏机理,并研究了肋板厚度和肋板高度对加筋板性能的影响。Zhou[12]等建立了加筋板弹性屈曲分析的解析解,研究了加筋板主要几何参数对其屈曲强度的影响。刘劲松[13]和任丽梅[14]等人对压弯成形进行了实验和数值模拟研究,分析了加劲肋的屈曲现象。然而,到目前为止,关于电脉冲辅助压弯成形整体壁板屈曲研究还很少。
本研究首先建立了Ti55钛合金整体壁板电脉冲辅助压弯成形的有限元模型,分析成形过程中壁板不均匀温度场分布及不同位置应力应变分布。并分析不同工艺参数和壁板几何参数对筋条失稳敏感性和筋条最终失稳程度的影响,为钛合金整体壁板电脉冲辅助压弯成形设计提供依据。
1、有限元模型
1.1几何模型和材料参数
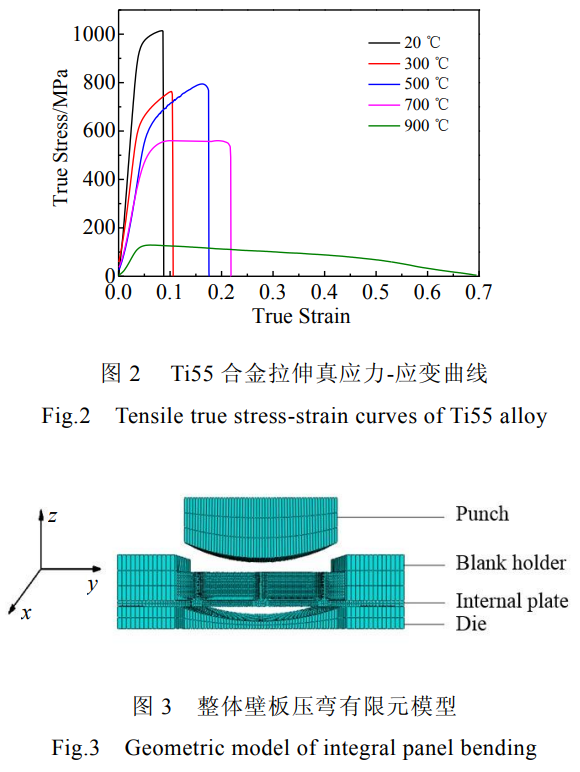
针对飞机整体壁板的典型结构,设计了一种多网格筋的整体壁板,整体壁板截面尺寸为100mm×50mm,厚度为12mm,其中蒙皮的厚度为2mm,加强筋宽度为1mm,加强筋之间横向宽度为21mm,纵向宽度为16mm,如图1所示。凹模长宽高相应为100mm×50mm×25mm,压弯半径分别为80、140、200mm,圆角过渡半径为10mm,压边区域长度为20mm。整体壁板材料为Ti55合金,其基本性能参数如表1所示。在拉伸机上进行了应变速率为0.01s-1单向拉伸实验,得到了不同温度下的应力-应变曲线如图2所示。模型中塑性参数的定义取曲线中的应力-应变数据。
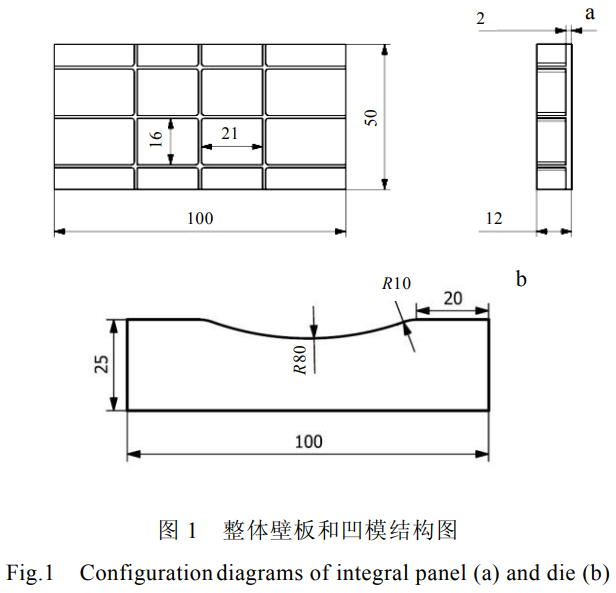
表1Ti55合金的热物理性能参数 Table1ThermophysicalperformanceparametersofTi55alloy
| Temperature/℃ | Thermalconductivity/W·m⁻¹·K⁻¹ | Specificheatcapacity/J·kg⁻¹·K⁻¹ | Coefficientoflinearexpansion/10⁻⁶K⁻¹ |
| 20 | 5.44 | 611 | 9.10 |
| 100 | 6.68 | 685 | 7.90 |
| 200 | 8.81 | 695 | 9.05 |
| 300 | 10.50 | 710 | 9.42 |
| 400 | 12.60 | 745 | 9.30 |
| 500 | 14.30 | 760 | 9.42 |
| 600 | 15.55 | 890 | 9.51 |
1.2模拟设置
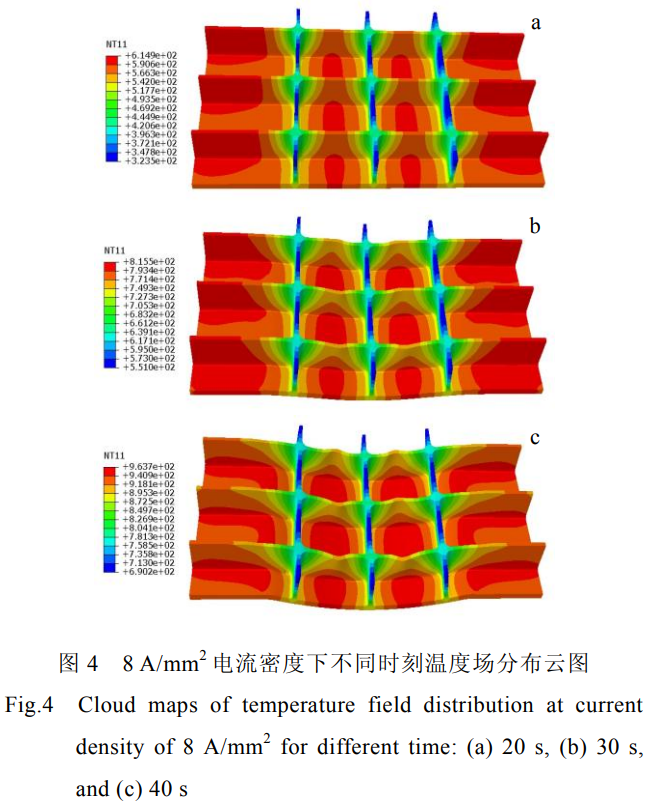
通过有限元商业软件ABAQUS热电结构耦合分析对Ti55网格筋整体壁板电脉冲辅助压弯过程进行数值模拟分析,建立的有限元模型如图3所示。凸模和凹模均定义为实体,筋板与模具、外界环境之间的换热系数设置为15W.m-2.K-1,设置凸凹模的表面为主面,板材的表面为从面。采用库仑摩擦条件,设置冲头、凹模以及压边块与筋板之间的摩擦系数为0.3。模拟过程中,凹模和压边块保持静止不动,各方向的位移均设定为零,在壁板横向两端施加电流,并对冲头施加指定速度加载条件,整个成形过程为40s,前20s为电脉冲加热阶段,后20s为压弯过程,后续压弯阶段电流继续对其加热。网格划分采用Q3D8R六面体单元,共有64274单元。
对5组不同工艺参数和几何参数加筋板压弯过程进行了有限元模拟,分析了工艺参数(施加电流大小和加筋板压弯半径)和几何参数(筋条宽高比、腹板厚度和横筋间距)对加筋板失稳屈曲的影响。各参数的取值范围分别为:电流密度(7~9A/mm²);壁板压弯半径(60~100mm);筋条高度(9~10mm);腹板厚度(1~3mm);横向筋条间距(11~41mm)。
2、结果与分析
2.1整体壁板温度场分析
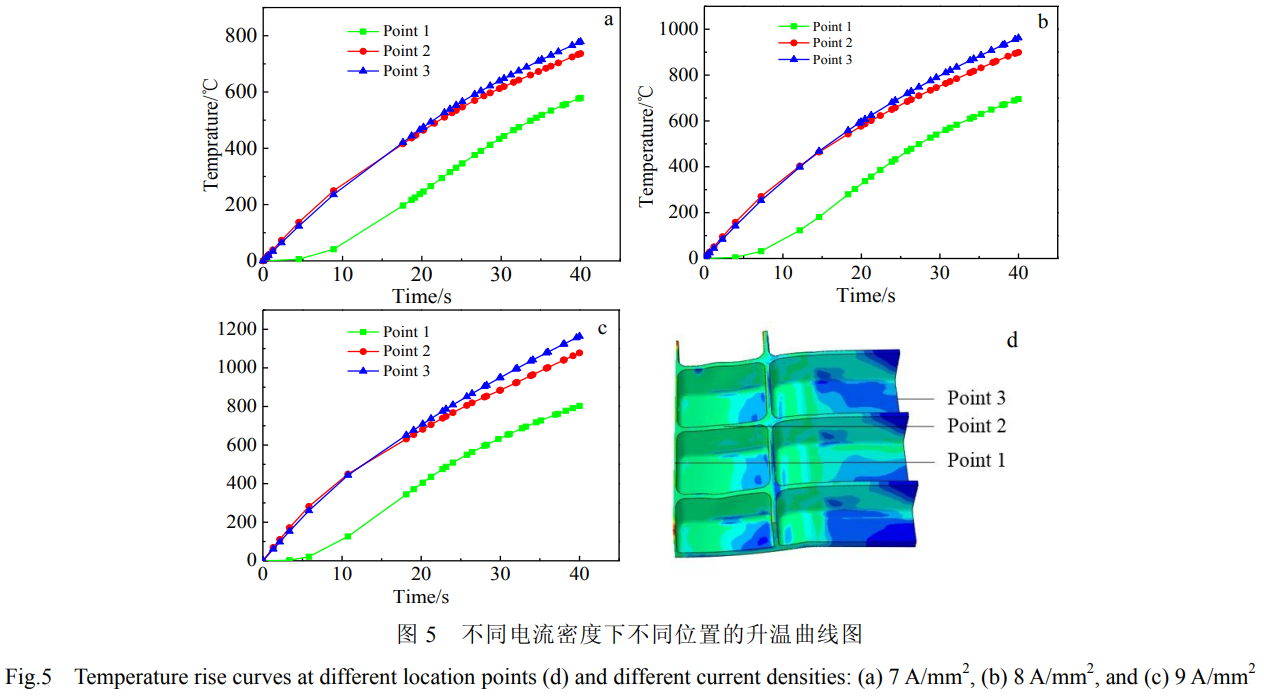
对施加电流密度7、8、9A/mm²的加筋板进行有限元模拟,图4为电流密度为8A/mm2时不同成形时间下的温度场分布云图。筋板横向中心区域的温度略高于两侧区域的温度,因为整体壁板的两侧始终和凹模、压边圈接触,壁板会向模具传热,从而导致中心区域的温度高于壁板两侧的温度。刚开始成形时,横向(y方向)筋条温度与腹板的温度相差不大,随着冲头的下压,横向筋条与冲头接触传热,导致最终成形时横向筋条温度比蒙皮温度低。由于电流施加方式是在壁板横向的两侧表面施加电流,纵向(x方向)筋条流经电流比横向筋条流经电流少,产生的焦耳热要少,纵向筋条处的温度远低于其他位置的温度。
在整体壁板筋条横筋处、筋条竖筋处、腹板中心处取3个温度分析点,如图5所示。从升温曲线图可以看出电流密度为7、8、9A/mm²时筋板压弯阶段的温度区间分别为494~786℃、615~963℃、727~1166℃。温度过低时Ti55合金成形较为困难,温度过高会导致氧化层的厚度较厚,当电流密度为8A/mm2时筋板压弯阶段所处温度区间最适宜。壁板蒙皮中心处(位置3)和横向筋条处(位置2)在前20s时温度一样,但在后20s时,冲头下压与壁板接触产生热传导,导致横向筋条升温速率下降,并且成形终了时横向筋条温度略低于腹板蒙皮处。由于整体壁板几何结构和电流加载方式,纵向筋条处区域温度要比其它处区域低很多。
2.2壁板压弯过程应力应变分析
图6所示为在8A/mm2电流密度不同时间下的应力应变分布云图。在成形的开始阶段(20s)时,壁板一直处于电流加热的状态,温度上升导致壁板热膨胀在中间位置产生一定的内应力。随着模具的下压,应力开始先增大,后面温度进一步的上升导致材料软化,应力反而呈下降的趋势。最终应力主要分布在压弯的中心线和两侧压边块的旁弯曲线上,并且由于纵向筋条温度较低,纵向筋条处等效应力值最大。在冲头刚与筋板接触时,筋板未开始变形,应变为零,随着变形的增加,等效应变不断增大,等效应变分布主要分布在横向筋条和凹模圆角区域,而纵向条处和腹板处几乎没有等效应变,表明其没有产生塑性变形。
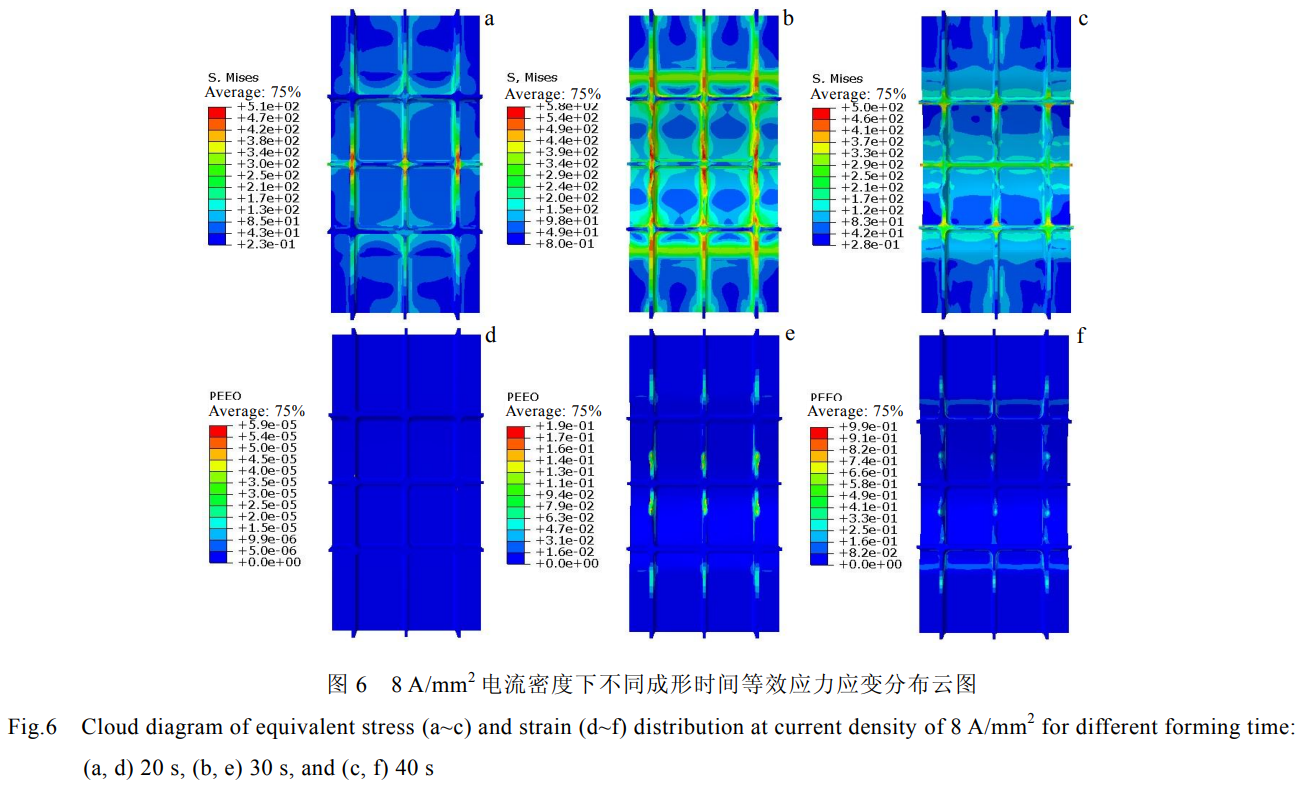
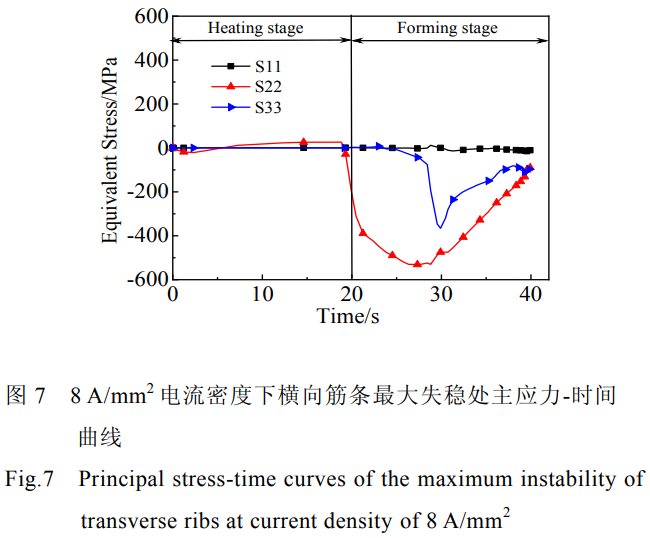
图7所示为8A/mm2电流密度下横向筋条最大失稳处主应力-时间曲线。由图7可以看出整体壁板横向筋条失稳处x方向主应力压弯过程中一直为零,随着冲头的下压壁板开始弯曲变形,横向筋条y方向压应力开始迅速增加,这也是横向筋条产生失稳的主要原因。随着壁板弯曲程度的加大,横向筋条z方向压应力也随着增加,后面由于横向筋条温度的上升,变形容易进行,应力值都呈下降的趋势。
2.3电流密度对壁板失稳屈曲的影响
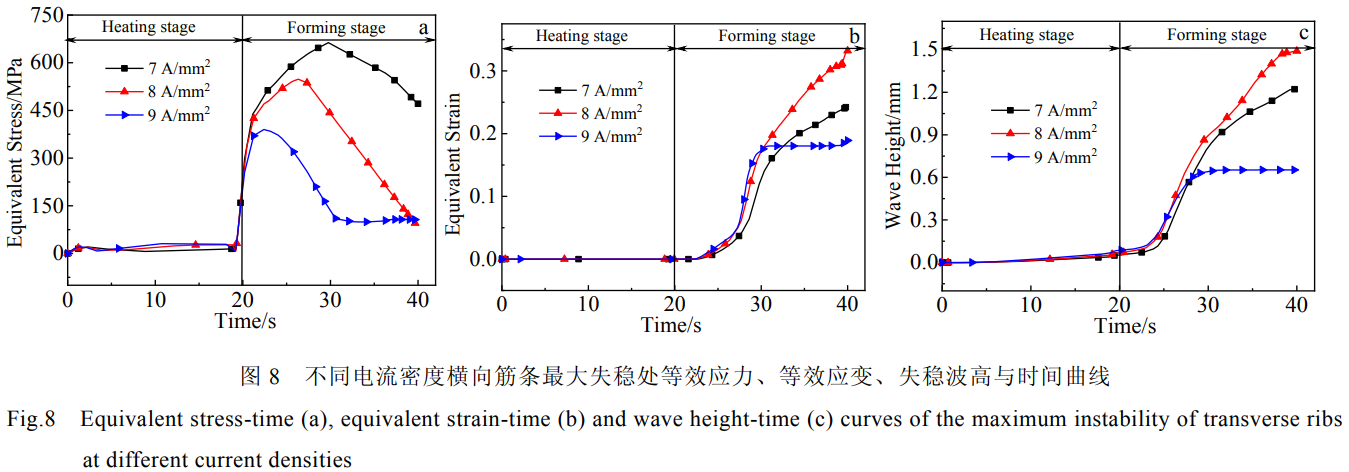
图8所示为不同电流密度下横向筋条失稳处等效应力、等效应变、失稳波高随时间的变化曲线。由图8a等效应力-时间关系图可知,在成形前20s时,由于筋板只处于加热阶段,筋板未开始变形,筋条处几乎无应力产生。电流加热导致温度的上升,整体壁板产生热膨胀,冲头实际和整体壁板接触的时间在19s。随着冲头的下压,应力变化整体趋势都是随着变形的增加,应力迅速上升,但是由于随着温度进一步的上升,材料软化导致应力下降。电流密度越大,升温速度越快,横向筋条失稳处的峰值应力随电流密度增加而减小。从图8b可以看出应变随电流密度增加先增大后减小。电流密度大,整体壁板温度高,筋条容易变形。但温度继续升高时,整体壁板直接被压弯,在横向筋条上的应力不足以让其变形。电流密度为9A/mm2时,成形的后10s中,应力应变几乎无变化,也就是在壁板压弯的最后10s过程中筋条没有发生塑性变形。从图8c可以看出,当整体壁板其余参数一致时,电流密度对筋条失稳开始的时刻没有影响,只有当壁板累计一定应变量时,筋条才开始发生失稳。
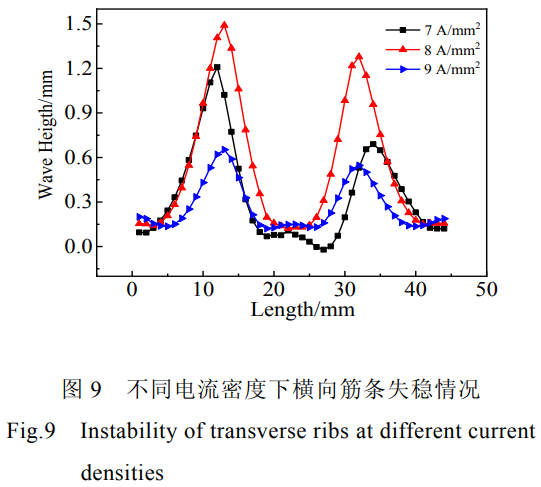
图9所示电流密度7、8、9A/mm²下壁板横向筋条沿x方向失稳距离的整体情况。电流密度7、8、9A/mm²时横向筋条最大失稳距离分别为1.07、1.37、0.65mm。随着电流密度增加,壁板筋条沿x方向失稳距离先出现增大趋势。壁板上筋条温度升高,筋条处应变较大,容易失稳屈曲。随着电流的进一步加大,壁板筋条失稳距离反而减小。温度上升,压弯所需的载荷减小,壁板筋条上的应力减小,导致应变相应减小,失稳屈曲程度减小。
2.4壁板压弯半径对失稳屈曲的影响
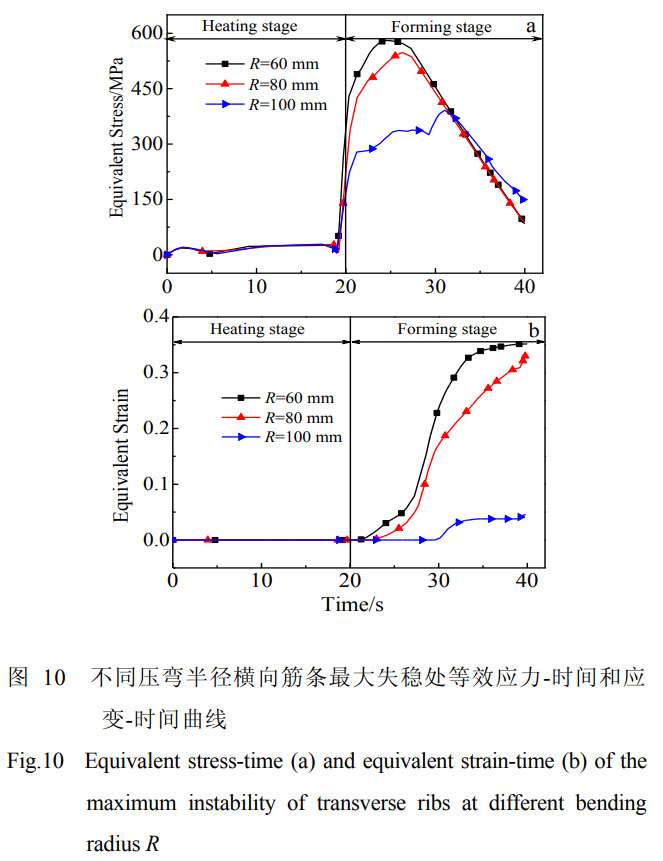
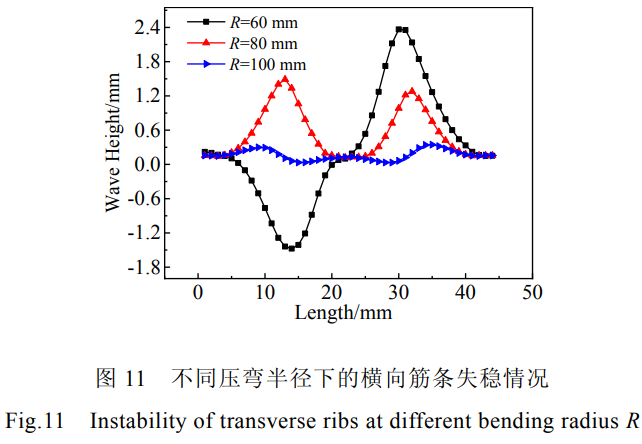
图10所示为不同压弯半径下横向筋条失稳处等效应力、等效应变随时间的变化曲线。由图10a可知压弯半径增加时,筋条应力也越来越小,筋条的受力情况得到相应的改善,筋条失稳程度减小。图10b为不同压弯半径下的筋条失稳处等效应变随时间关系,压弯半径为60、80、100mm时筋条失稳处的最终等效应变分别为0.36、0.32、0.05,压弯半径增加,筋条的变形量随之减小。由图11不同压弯半径下的横向筋条失稳情况可知,整体壁板压弯时,随着压弯半径的减小即变形量的增大,筋条失稳越来越严重,横向筋条失稳程度越来越大,这与筋条失稳处的等效应变结果相吻合。压弯半径越小,横向筋条失稳屈曲程度越严重,筋条失稳形成的半波的幅值越大。
2.5筋条宽高比对壁板失稳屈曲的影响
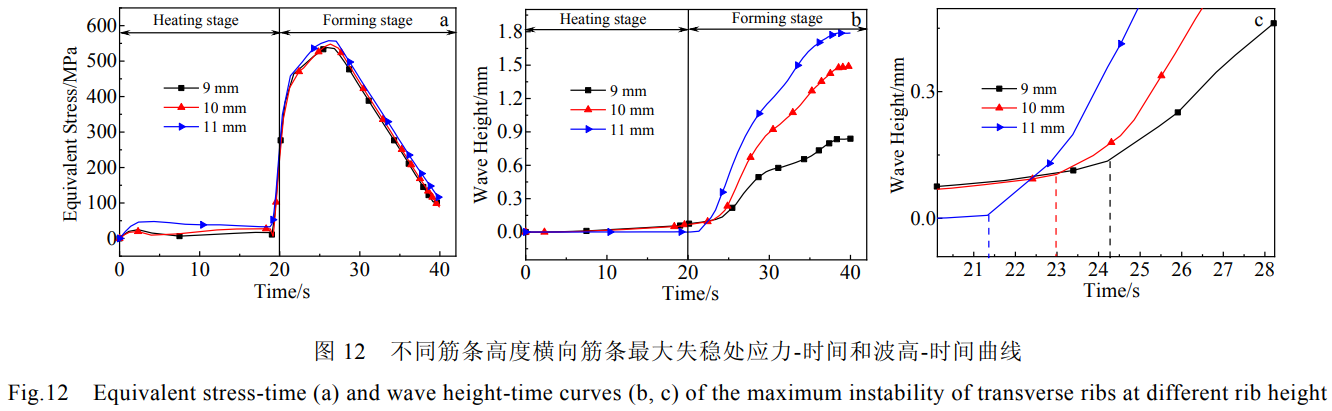
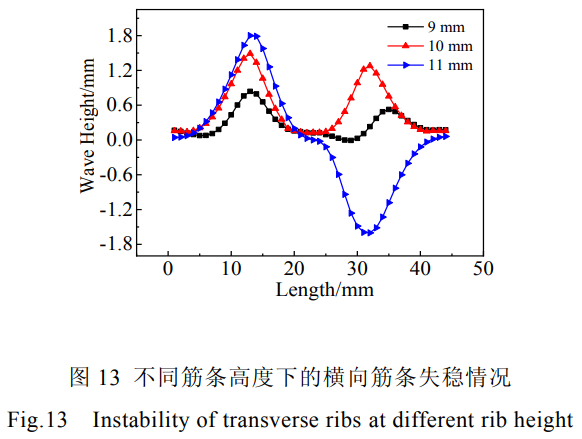
图12所示为不同筋条高度横向筋条最大失稳处等效应力、波高-时间曲线。由图12a等效应力-时间关系可知,筋条高度对横向筋条最大失稳处应力无明显影响。图12b所示筋条宽高比对失稳时刻的影响,图12c为12b的局部放大图,由图可以看出,筋条高度为9~11mm时横向筋条开始发生失稳的时间分别为24.21、23、21.33s,筋条高度越高,壁板开始的失稳的时间也越早。这表明筋条高度越高筋条失稳时所需的临界载荷越小,发生失稳的时间越短,整体壁板筋条的稳定性较差。图13为不同筋条宽高比下的横向筋条失稳情况。由图可知,在整体壁板筋条厚度不变,随着筋条高度的增加,筋条失稳屈曲程度越来越大。
2.6腹板厚度对筋条失稳屈曲的影响
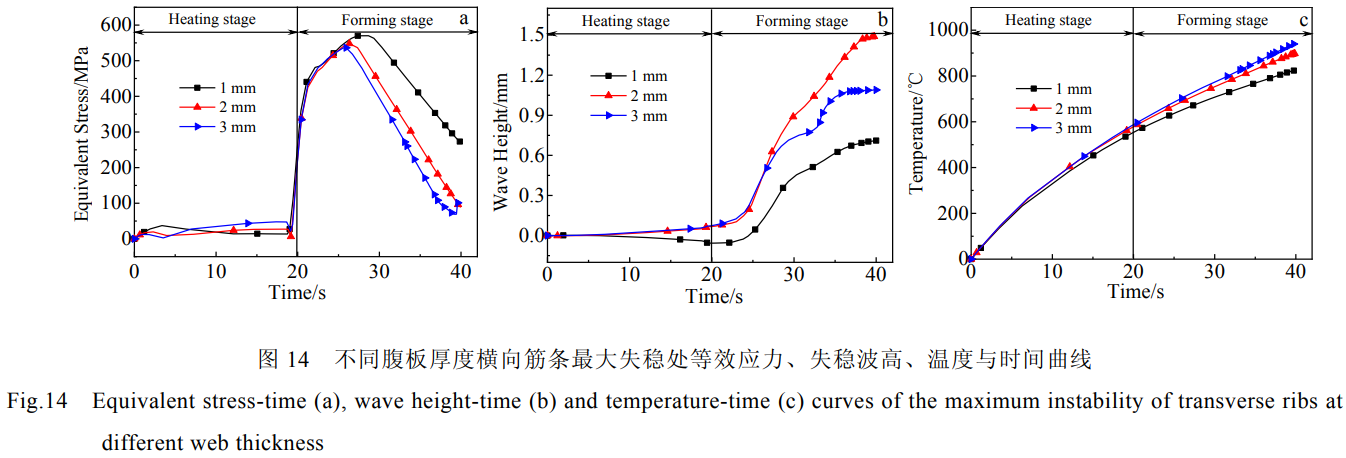
图14所示为不同腹板厚度下横向筋条最大失稳处等效应力、失稳波高和温度随时间变化的曲线。由图14a可知,不同腹板厚度的壁板在发生失稳时的筋条处的应力相同。由图14b可以看出,腹板厚度不同,筋条失稳时刻均发生在24s左右,无显著差异,所以腹板厚度不会对筋条的失稳时刻产生影响。由图14c可知随着腹板厚度的增加,壁板散热减少,筋条温度上升。
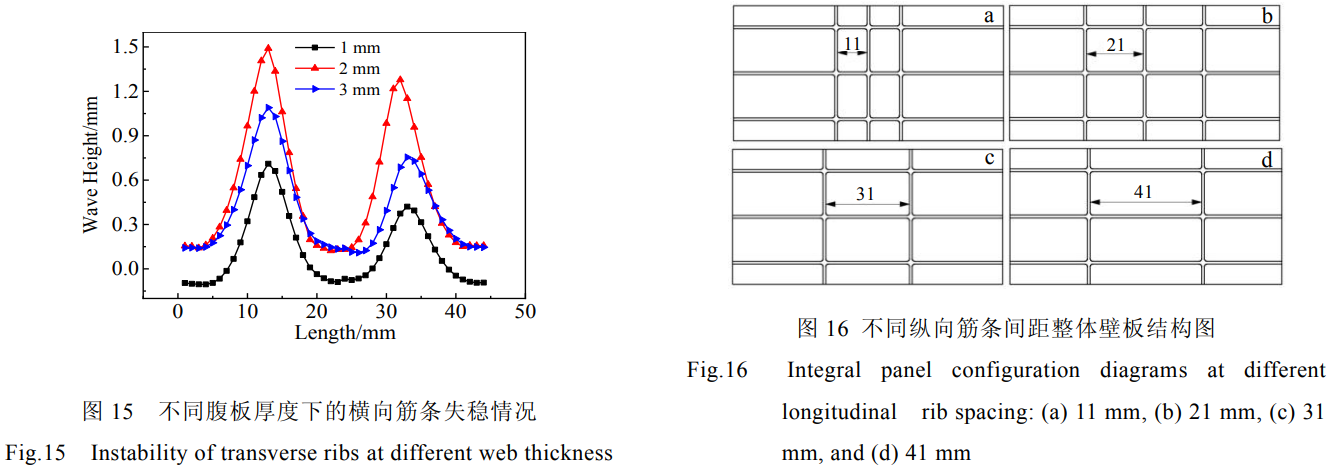
图15为不同腹板厚度下的横向筋条失稳情况。腹板厚度增加,筋条失稳屈曲程度加大,腹板厚度进一步增加,壁板散热减少,导致温度上升,成形壁板所需载荷减小,壁板筋条上应力减小,失稳屈曲程度反而有所减小。腹板厚度其实影响筋条的温度从而影响筋条失稳的变化。
2.7纵向筋条间距对壁板失稳屈曲的影响
图16为不同纵向筋条间距整体壁板结构图。图17所示为不同纵向筋条间距下横向筋条最大失稳处等效应力、失稳波高和温度随时间变化的曲线。由图17可知纵向筋条间距为41mm时壁板筋条发生的失稳时刻要比31mm早很多,从应力-时间关系图可以看出,纵向筋条间距为41mm时壁板筋条发生的失稳时刻应力也小很多,纵向筋条间距越大,横向筋条稳定性越差。纵向筋条的数量越少,电流向纵向筋条分流减小,横向筋条温度越高。筋条间距由31mm增至41mm而纵向筋条数量没有变化时,横向筋条处温度无明显差别。
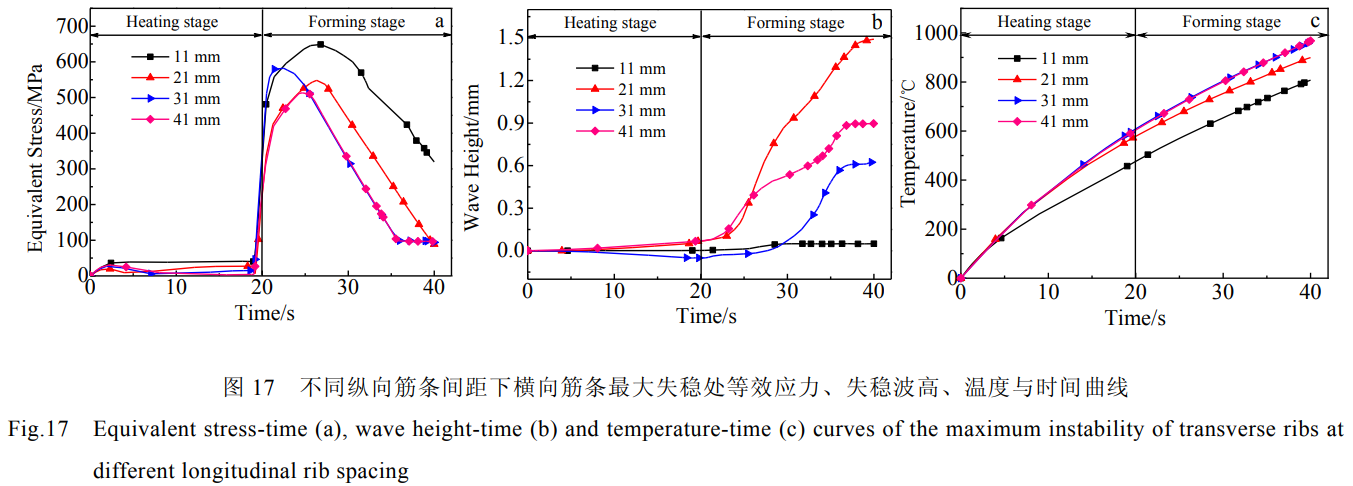
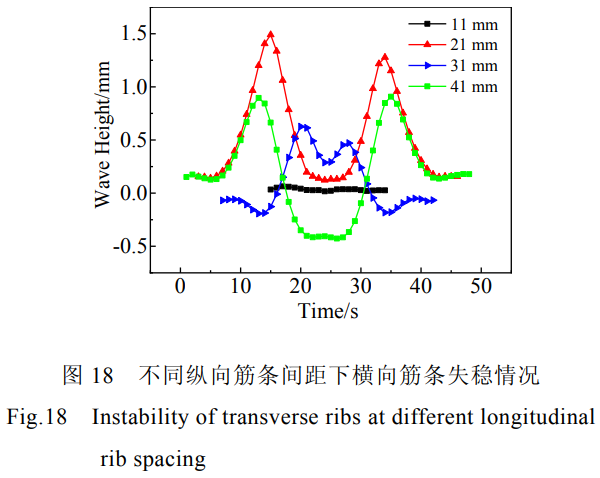
图18所示为不同纵向筋条间距下的横向筋条失稳情况。由图18可知,当纵向筋条间距为11mm时,整体壁板没有产生失稳弯曲,纵向筋条的存在阻碍了横向筋条的变形,使整体壁板变形更均匀。筋条间距由21mm增至31mm时,筋条温度过高时,且压弯中心线处无纵向筋条,整体壁板中心处受力情况得到改善,失稳程度反而减小。压弯中心线处无纵向筋条时,纵向筋条间距越大,横向筋条越容易失稳,成形最终失稳程度越大。
3、结论
建立了Ti55合金通电压弯的电-热-结构多场耦合模拟模型并进行模拟,对施加不同电流密度的整体壁板温度场进行分析,为获得Ti55合金合适的成形温度和避免温度过高壁板氧化严重,在壁板端施加8A/mm2电流密度能获得合适的压弯温度区间。
整体壁板随着筋条高度的增加,筋条失稳屈曲程度越来越大。筋条高度越高,筋条开始的失稳的时间也越早,筋条失稳时所需的临界载荷越小,发生失稳的时间越短,筋条的稳定性越差。
腹板厚度主要是影响筋条的温度从而影响壁板压弯过程中筋条的失稳,这与电流密度对筋条失稳的影响相类似。
整体壁板纵向筋条间距增大,筋条稳定性越差,筋条失稳屈曲也越严重。
参考文献 References
[1] Zhao Anan (赵安安), Zhang Xianjie (张贤杰), Gao Guoqiang (高国强) et al. Acta Aeronautica et Astronautica Sinica (航空学报)[J], 2019, 40 (2): 197
[2] Xu Aijun (许爱军), Jia Yuerong (贾悦荣), Zhang Changxi (赵长喜). Manned Spaceflight (载人航天)[J], 2017, 23 (5): 619
[3] Lang Lihui (郎利辉), Xu Aijun (许爱军). Aviation Precision Manufacturing Technology (航空精密制造技术)[J], 2011, 47 (2): 30
[4] Liu Zhangguang, Li Peijie, Xiong Liangtong et al. Materials Science & Engineering A [J], 2017, 680: 259
[5] Grimm Tyler J, Ragai Ihab. Procedia Manufacturing [J], 2019, 34: 118
[6] Liu Kai, Dong Xianghuai, Shi Wen et al. Journal of Shanghai Jiaotong University, Science [J], 2019, 24 (4): 409
[7] Yan Yu, Wang Haibo, Wan Min. Transactions of Nonferrous Metals Society of China [J], 2011, 21 (11): 2459
[8] Yan Yu, Wang Haibo, Wan Min. Computational Materials Science [J], 2011, 50 (7): 2232
[9] Mallela Upendra K, Upadhyay Akhil. Thin-Walled Structures [J], 2016, 102: 158
[10] Li Shen, Hu Zhiqiang, Benson Simon. Engineering Structures [J], 2019, 199: 109627
[11] Su Yuru, Guan Zhidong, Wang Xin et al. Chinese Journal of Aeronautics [J], 2019, 32 (3): 619
[12] Zhou Wenbin, Li Yong, Shi Zhusheng et al. International Journal of Mechanical Sciences [J], 2019, 161-162: 105024
[13] Liu Jinsong (刘劲松). Thesis for Doctorate (博士论文)[D]. Shenyang: Institute of Metal, Chinese Academy of Science, 2004: 27
[14] Ren Limei (任丽梅), Wang Zhongtang (王忠堂), Liu Jinsong (刘劲松) et al. Journal of Plasticity Engineering (塑性工程学报)[J], 2003, 10 (5): 39
(原文标题:Ti55钛合金整体壁板电脉冲辅助压弯成形失稳研究)
无相关信息
